Use numeric patterns to make generalizations about properties of polygons.

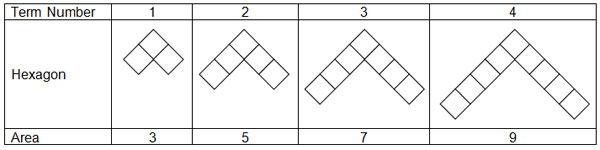
Which of the following expressions represents the area of each hexagon in terms of the term number?

A. 2n
Incorrect. The rate of change in the area for each series number is 2, but how does the area relate to the term number itself?

B. n + 2
Incorrect. The area increases by 2 each time, but how does the area relate to the term number?

C. 2n + 1
Correct! In each figure, there is a starting square at the apex, and 2 congruent branches with the same length as the term number.

D. 2n – 1
Incorrect. If each term number is doubled, what do you need to add or subtract in order to find the area?

Suzanne used the dynamic geometry sketch of a regular hexagon, shown in the figure, to investigate the relationships among the radius, apothem, and side length of regular hexagons.

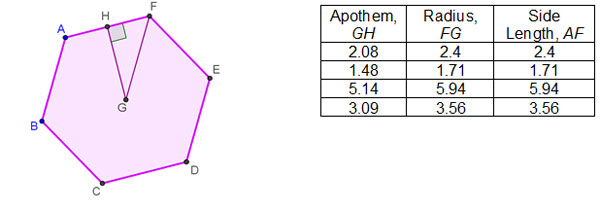
Based on the information in the table, which of the following statements is NOT true for this regular hexagon?

1. The apothem is always the largest of the three segments.
   Correct! The apothem is actually the smallest of the three segments for any regular hexagon. This statement is the only one given that is not true.
2. The radius and the side length are always the same.
   Incorrect. Examine the data in the table to compare the radius and the side length.
3. The radius, apothem, and half of the side length will always form a 30-60-90 triangle.
   Incorrect. The measure of the central angle (between two radii) in a hexagon is 60°. Examine the figure to determine the measure of the remaining angle.
4. The apothem is always shorter than the radius.
   Incorrect. The shortest distance between a point and a segment is always the perpendicular distance.

The table below shows a series of regular polygons with all diagonals drawn from one vertex.

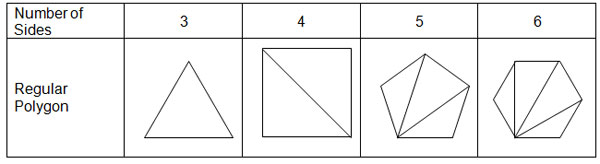
Based on the information in the table, which of the following statements is true?

1. All of the triangles created by the diagonals are obtuse.
   Incorrect. What kind of triangles are created by the diagonal in the square?
2. All of the triangles created by the diagonals are equilateral.
   Incorrect. What kind of triangles are created by the diagonal in the square?
3. The number of diagonals that can be drawn from any one vertex is equal to 3 more than the number of sides in the regular polygon.
   Incorrect. Compare the number of diagonals in the square to the number of sides in the square.
4. The number of diagonals that can be drawn from any one vertex is equal to 3 less than the number of sides in the regular polygon.
   Correct! Any polygon has 3 vertices that cannot be the endpoints of a diagonal from a given vertex: the vertex itself and both adjacent vertices.

Mary watched her daughter construct the following pattern from blocks that are made up of congruent isosceles triangles.

Which expression could Mary use to determine the perimeter of a composite figure made up of t of these isosceles triangle blocks?

1. 14t
   Incorrect. When 2 or more triangles are connected, which sides are no longer part of the perimeter?
2. 12 + 2t
   Correct! Each composite figure has two sides with length 6 each, and t sides with length 2 each.
3. 12t + 2
   Incorrect. In each of the composite figures shown, what changes, and what stays the same?
4. 6t + 2(2t)
   Incorrect. What happens to the number of bases of isosceles triangles as more triangles are added to the composite figure?